This page contains a bond pricing calculator which tells you what a bond should trade at based upon the par value of the bond and current yields available in the market (sometimes known as a yield to price calculator).
It sums the present value of the bond's future cash flows to provide price. It returns a clean price and dirty price (market price).
Bond Pricing Calculator with Dirty Price and Clean Price
Using the Bond Price Calculator
Inputs to the Bond Value Tool
- Bond Face Value/Par Value - Par or face value is the amount a bondholder will get back when a bond matures.
- Annual Coupon Rate - The annual coupon rate is the posted interest rate on the bond. In reverse, this is the amount the bond pays per year divided by the par value.
- Market Rate or Discount Rate - The market rate is the yield that could otherwise be received by buying another investment. Generally, this will be different than the actual coupon rate on a bond - see our bond yield to maturity calculator for more (this is essentially the inverse of this operation).
- Years to Maturity - The number of years remaining until the bond pays out the face value. You may use decimals here - 9 years and 6 months is 9.5 years, for example.
- Days Since Last Payout - Enter the number of days it has been since the bond last issued a coupon payment into this field of the bond pricing calculator.
- Coupon Payout Frequency - How often the bond makes a coupon payment, per year. If it only pays out at maturity try the zero coupon bond calculator, although the tool can compute the market price too.
Bond Price Tool Outputs
- Dirty Price - Dirty price is the actual predicted market trading price of the bond with characteristics matching the input. It differs from the clean price because yield can be thought to 'compound continuously', but payments themselves only come periodically. If you aren't buying or selling a bond on the date it is making a payment that means there is some implied interest on the bond.
- Clean Price - Clean price is the price of the bond if accrued interest is ignored. This calculation relies only on the difference between market price and the coupon rate of the bond.
- Accrued Interest - For convenience, we have explicitly calculated the amount of the market price that is due to accrued interest. If you subtract this from the dirty price you get the clean price.
Calculating Accumulated Interest
Accumulated interest on a bond is easy to calculate. The only trick is a shortcut due to the day count convention; we assume here a round number of days for the various periods which don't exactly match the calendar. If the slight error doesn't match the payments on your bond, we suggest you calculate them on your own using our guidelines but substituting for your inputs.
Anyway, this is what we are using for 'the time between payments' internally to the bond pricing calculator:
- ONE YEAR = 360 Days
- TWICE A YEAR = 180 Days
- ONCE A QUARTER = 90 Days
- ONCE A MONTH = 30 Days
- NONE = At Maturity (Zero Coupon Bonds)
The accrued interest formula is:
F * (r/(PY)) * (E/TP)
Where:
- F = Face value of the bond
- r = Coupon rate
- PY = Payments a Year
- E = Days elapsed since last payment
- TP = Time between payments (from above description).
Using the example in the calculator, but with 45 days elapsed:
1000 * (.1/2) * (45/180) = $12.50
The Dirty Price and Clean Price Formulas
As in our yield to maturity calculator, this is a hard problem to do by hand. The trading price of a bond should reflect the summation of future cash flows. Let us first show how this is done in a spreadsheet program.
Calculating Clean Bond Price Using Microsoft Excel or OpenOffice
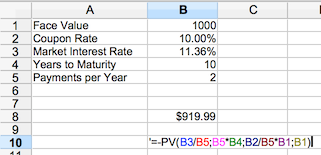
You will want to start by creating a spreadsheet such as the above. nclude the parameters we have in the calculator on this page - Face Value, Coupon Rate, Market Interest Rate (or Discount Rate), Years to Maturity and Payments per Year. Then you should use the 'PV' formula (use ';' to separate inputs in OpenOffice, use ',' in Excel). The PV formula works like this:
- Rate (Divide by payouts a year)
- Number of Periods (Payouts per year multiplied by years)
- Payment (Annual payment divided by payouts per year)
- Future Value (Face Value)
... as you can see in the above screenshot.
The Present Value Formula
'PV' is, of course, the present value formula. Present value is the concept we hinted to above - the value of a stream of future payments discounted by the conditions in the market today.
Present value, then, is a summation. You can write out each cash flow by hand and calculate it, but this is where computers thrive - feel free to work through some examples with this formula, but know that spreadsheet programs and the JavaScript calculator above are much faster at this sort of work! Here's the formula courtesy Wikipedia:
Where:
- C = amount of the cash flow to discount
- n = number of periods
- i = interest rate
Calculating Dirty Price
Luckily, dirty price is very simple to calculate - you merely calculate the value of the clean price and add the accumulated interest. (And yes, that's as easy as it gets in finance. )
Either way, now you know a lot more about what drives bond pricing in the market - and you have a little more clarity about the theory behind the numbers. Hope you enjoyed the bond pricing calculator and the explanations for how we are calculating the clean and dirty price!
What's next?
Try our other financial basics and valuation calculators: